高等代数与解析几何知识点

线性空间
- 定义, 常见的例子: 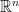$\mathbb{R}^n$ , 多项式, 连续函数等组成的空间…
- 从已知线性空间构造新的线性空间: 子空间, 商空间, 直和, 线性映射的核空间/像空间, (线性映射组成的空间 $\mathop{Hom}(V,W)$ , 对偶空间 $V^*= \mathop{Hom}(V,K)$ , 直积, 张量积, 外积… )
线性映射
- 选定一组基以后, 线性映射 $\Leftrightarrow$ 矩阵. 换不同的基 $\Leftrightarrow$ 矩阵的相似变换.
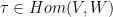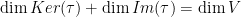
- 维数公式: $\tau\in \mathop{Hom}(V,W)$ , 则 $\dim \mathop{Ker}(\tau) + \dim \mathop{Im} (\tau) = \dim V$
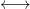- 不变子空间 $\longleftrightarrow$ 存在基使得在这组基下线性映射成分块上(下)三角形;
- 空间的分解成不变子空间的直和 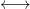$\longleftrightarrow$ 存在基使得在这组基下线性映射成分块对角矩阵;
- 特征值, 特征向量, 矩阵/线性变换可对角化 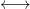$\longleftrightarrow$ 存在一组由特征向量组成的基
- 任意有限维空间上的线性变换有若当标准型, (幂零)若当块 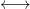$\longleftrightarrow$ 循环子空间, 幂零变换的若当标准型, 广义特征子空间
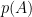- 矩阵(线性变换的)函数(多项式或幂级数): 对多项式 $p$ 可以定义 $p(A)$ , 可以定义矩阵的指数 $e^A$ , (事实上如果矩阵可对角化, 可以对任意连续函数可以定义矩阵函数Functional calculus…)
- 用若当标准型计算 $g(A)$
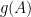
带有附加配对(paring)结构的线性空间, (Paring: 线性空间上的对称、共轭对称或反对称的非退化双线性函数)
- (伪)内积,酉内积,辛内积 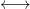$\longleftrightarrow$ 欧氏空间, (伪)欧氏空间,酉空间,辛空间
- (酉)内积空间中的Cauchy-Schwarz不等式, 三角不等式
- 任取基, 得度量矩阵:
  内积, (伪)内积, 酉内积, 辛内积分别对应正定对称矩阵, 可逆的对称矩阵, 正定的共轭对称矩阵, 反对称矩阵
- 换基 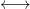$\longleftrightarrow$ 矩阵的合同(congruence)变换 (即 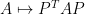$A\mapsto P^TAP$ 或(在酉空间中) $A\mapsto P^*AP$ )
- 存在特别的基: 标准正交基(对欧氏空间, 酉空间), 辛空间(辛基), 对应的度量矩阵特别简单 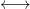$\longleftrightarrow$ 矩阵
- 标准正交基的构造: Gram–Schmidt方法 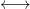$\longleftrightarrow$ (可逆)矩阵的QR分解(即分解为正交矩阵和上(或下)三角矩阵的乘积)
- 保持结构的线性变换/矩阵(这些变换组成一个群): 正交变换/矩阵, 酉变换/矩阵, 辛变换, (伪内积空间上可以定义类似的变换)
- 非退化的配对结构 $\leadsto$ Adjoint/Transpose的概念
- 谱理论: 对称变换/矩阵(或正规变换)可以在某个标准正交基/用某个正交矩阵(或酉矩阵) 对角化;
  半正定矩阵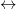 $\leftrightarrow$ 对角线上非负数 (所以这样的矩阵可以求”开方”),
  Hermit矩阵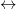 $\leftrightarrow$ 对角线上实数,
  酉矩阵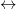 $\leftrightarrow$ 对角线上是单位根
  正交矩阵的标准形(分块对角矩阵, 每一块要么是 $\pm 1$ 要么是个旋转.
- 其他的常见分解: 极分解(Poler decomposition), (SVD分解…)
- (伪内积空间与内积空间的异同, 不同, 如存在长度为零的非零向量.)
多项式环, 整数环, (一般的环的概念, 交换环, 零因子, 整环等概念…)
- (多项式)环的理想的概念, 主理想的概念, 一元多项式环与整数环是主理想整环, 多元多项式环不是
- 最大公因子/互素, 最小公倍数的概念及其与对应的理想的关系; 环中的单位(unit即可逆元)的概念, 不可约元/素元/(素理想)的概念, 唯一分解整环/唯一分解定理, 整数环是唯一分解整环(算术基本定理), (一元或多元)多项式环是唯一分解整环.
- 中国剩余定理(和它的环论描述)
- 多项式环中的因式分解:
  在复数域上分解为一次多项式的乘积(代数基本定理), 重根的概念, 及重根重数的判定法则
  在实数域上, 分解为一次或二次多项式的乘积.
  有理数域/整数环上, 分解为本原多项式的乘积, (一类本原多项式不可约的判别法: Eisenstein判别法)
- 整数环, 整数环的商环(即同余类组成的环), Euler函数(另一种看法: $\mathbb{Z}/n\mathbb{Z}$ 中可逆元的个数)和它的计算公式, (积性函数Multiplicative function的概念), Euler定理/Fermat小定理
- (用一元多项式环进一步理解线性变换的不变子空间/Jordan标准型的理论.)
- (多元多项式环这的”首项”的概念, 初等对称多项式, 根与系数关系, 对称多项式基本定理, 判别式, 指数和/牛顿关于初等对称多项式与指数和之间关系的等式)
解析几何
- 仿射空间, 度量空间, 射影空间的概念;
- 选取仿射标架,正交标架(射影坐标系) 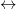$\leftrightarrow$ 将空间等同于 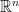$\mathbb{R}^n$ (或 $P(\mathbb{R})^n$ )
  保持结构的变换: 仿射变换, 保距变换, (射影变换);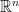 $\mathbb{R}^n$ (或 $P(\mathbb{R})^n$ )上这些变换的矩阵表达形式
  换标架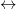 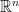$\leftrightarrow$ $\mathbb{R}^n$ 上的仿射/保距变换.
- (Klein和Erlangen纲领:几何=研究变换下的不变量)
- 方程和图形: 一般方程, 参数方程
  二/三维空间中的例子: (三维空间中的特殊工具:外积(叉积,cross product))
  直线, 平面的的方程
- 二次曲线和二次曲面:
  典型的二次曲线和二次曲面的方程和图形
  二次曲线、曲面的等距分类/仿射分类/射影分类 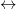$\leftrightarrow$ 本质上是对称矩阵在不同变换下的等价类.
  二次曲面与平面的截线
  典型的非平凡的直纹面: 单叶双曲面, 双曲抛物面
- (用仿射变换/射影变换证明平面几何中的问题…)